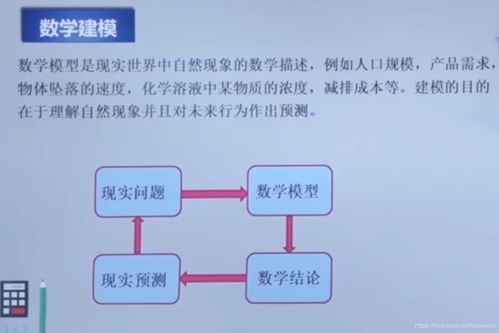
本课程是人工智能数学基础系列的第一部分，重点回顾初等函数核心性质，并系统介绍函数极限定义、极坐标与参数方程表示法。这些概念是后续机器学习、深度学习算法的理论基础。

一、初等函数核心性质回顾

1. 有界性

函数在定义域内取值存在上下界。例如：正弦函数y=sin x在[-1,1]内有界。在AI中，激活函数（如Sigmoid）的有界性确保神经元输出稳定。

2. 单调性

函数在区间内保持递增或递减趋势。ReLU激活函数在x>0时严格递增，这是深度学习模型收敛的关键性质。

3. 奇偶性

奇函数满足f(-x)=-f(x)，偶函数满足f(-x)=f(x)。卷积神经网络中的滤波器设计常利用此性质。

4. 周期性

函数值按固定周期重复出现。傅里叶变换处理时序数据时，周期性分析至关重要。

二、函数极限的精确定义

采用ε-δ语言严格定义：对任意ε>0，存在δ>0，使得当0<|x-x0|<δ时，|f(x)-L|<ε成立。这个定义是梯度下降法、反向传播等优化算法的理论基础。

三、极坐标与参数方程

极坐标表示

点位置用(r,θ)表示，其中r为极径，θ为极角。在计算机视觉中，极坐标常用于图像旋转不变性处理。

参数方程

曲线用参数t表示：x=x(t), y=y(t)。机器人运动轨迹规划、三维建模都依赖参数方程。

四、人工智能软件开发应用

掌握这些数学工具后，开发者能够：

1. 设计合适的激活函数和损失函数
2. 实现优化算法的收敛性分析
3. 处理计算机视觉中的几何变换
4. 构建稳定的数值计算程序

建议配合Python的NumPy、SymPy库进行实践练习，将理论知识与实际编程相结合。